Goldbach Weave
|
On Prime NumbersGoldbach's conjecture relates to a branch of mathematics known as number theory which deals with prime numbers. A prime number is a number that cannot be divided by any other number except 1 and the number itself. 13 is a prime number, for example, because it can only be divided by 1 (to get 13) or by 13 (to get 1). 15 is not a prime number, being divisible by both 3 and 5. Note that when we talk about numbers here we really mean whole numbers (known as integers or natural numbers). Of course it is possible to divide any number by any other number, but we're only interested in results that don't leave any fractions. For example, you can divide 15 by 6, for example, but you end up with 2½ (or 2.5 in decimal notation). That's clearly not an integer so it doesn't interest us here. |
Goldbach's original conjecture (known as the "ternary" Goldbach conjecture) was stated in a letter he wrote to Euler in 1742:
|
|
Every number that is greater than 2 is the sum of three primes
-- Christian Goldbach
|
|
In this case he was treating the number 1 as a prime number but we no longer follow that convention today. Euler re-stated it in the more familiar form now known as the "binary" or "strong" Goldbach conjecture:
|
|
All positive even integers greater than 2 can be expressed as the sum
of two primes
-- Euler, restating Goldbach's conjecture
|
|
The conjecture can be written algebraically as follows:
2n = p + qHere, p and q are both primes numbers. n is a natural (whole) number, and 2n is therefore an even number. If we divide both sides of the equation by 2, we get the following:
p + q
n = -----
2
So another way of expressing Goldbach's conjecture is as follows:
|
|
Every integer greater than 1 is the average of two prime numbers.
-- Wardley, restating Euler restating Goldbach
|
|
Despite being over 250 years old, Goldbach's conjecture remains unproven. It has been tested for the first few billion numbers and no-one has ever found a counter-example. Most mathematicians believe it to be true, but no-one has ever proved it. And so it remains a conjecture.
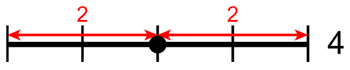
The different ways in which an even number can be composed of 2 prime numbers are known as Goldbach Partitions. The diagram below represents the number 4, indicated by the horizontal line divided into 4 equal segments. The one and only Goldbach partition of 4 is 2 + 2, shown by the red arrows. The black dot is added at the partition point.
The next diagram shows the single Goldbach partition for the number 6: 3 + 3.

The number 8 is summed from the prime numbers 3 and 5. Of course it doesn't matter which way round you add numbers because 3 + 5 is the same as 5 + 3. However, we show both points for completeness and to make the diagram nicely symmetrical.

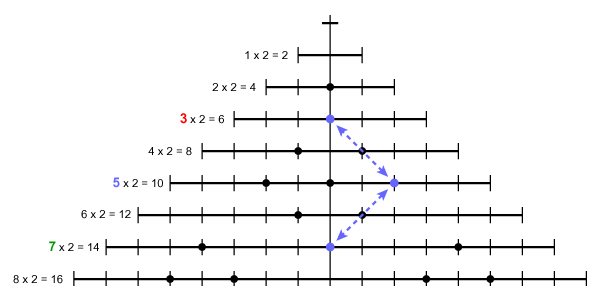
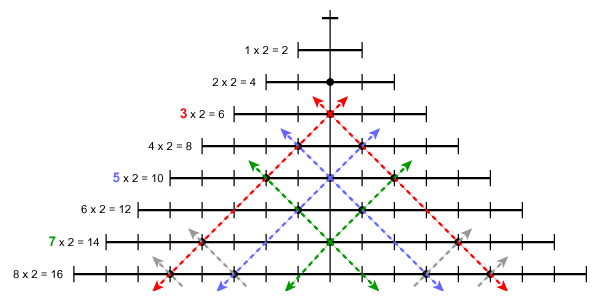
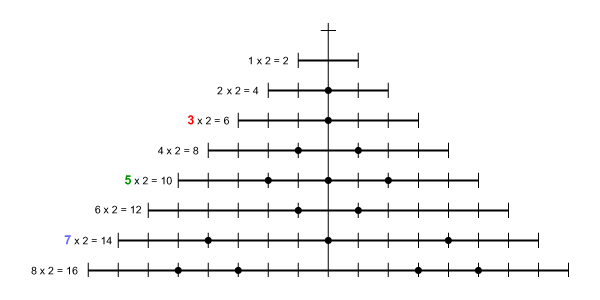
The next diagram shows the first few numbers composed into a single diagram. Notice how the dots running down the centre vertical line correspond to the prime numbers (or in this case, twice the prime number), e.g. 2 (2 + 2 = 4), 3 (3 + 3 = 6), 5 (5 + 5 = 10), 7 (7 + 7 = 14), and so on. The large picture at the top left of this page is the complete weave of the first hundred or so integers (although rotated through 90° to make it fit the page better).
Each prime number starts a new thread of prime numbers that continue to infinity.
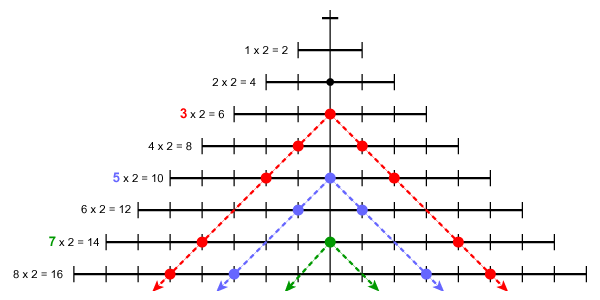
Each thread of prime numbers running along the warp intersects with the threads of prime numbers running back along the weft.
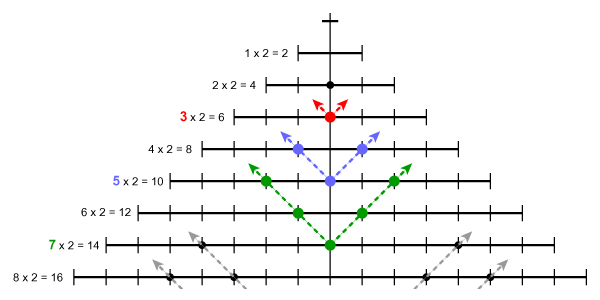
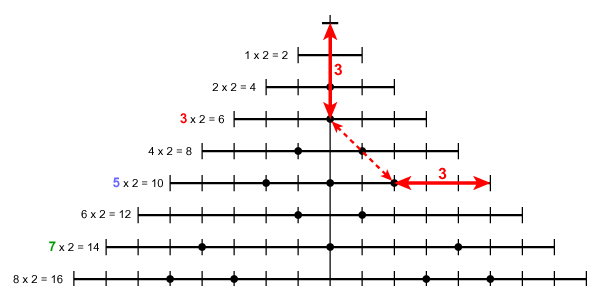
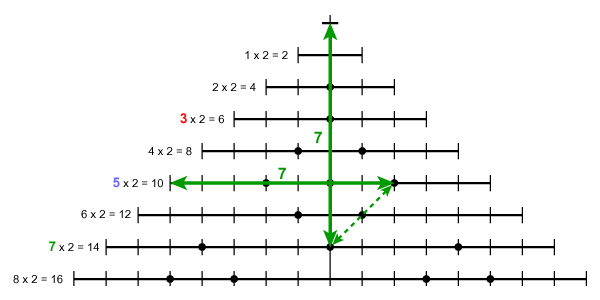
The following two diagrams illustrate one of the Goldbach partitions for the number 10: 3 + 7. The red dots and lines represent the number 3, the green dots and lines, the number 7. In both cases, the numbers can be read from left-to-right or from top-to-bottom. It doesn't matter - it's all the same thing.
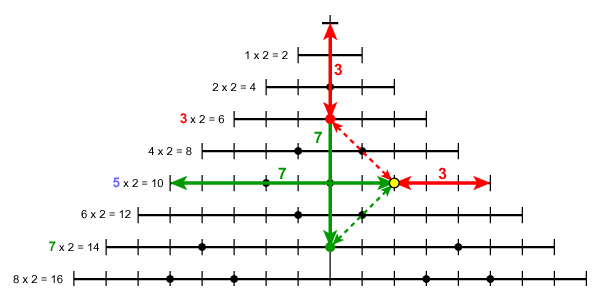
This final diagram shows how the Goldbach partition for 10 (3 + 7) can be re-phrased as "the number 5 is half-way between 3 and 7".