Newcomb's Paradox
Scott Aaronson recently blogged on the subject of Newcomb's Paradox. This hypothetical scenario involves an omnipotent being (the Predictor) who can somehow predict with 100% accuracy what you're going to do in advance of you actually doing it.
His Mighty Predictorness offers you two boxes: one containing $1,000 and the other with either $1,000,000 or nothing. If the Predictor thinks you're planning to open the $1,000 box (and he's never wrong) then he'll leave the other box empty and you'll pocket only $1,000. On the other hand, if you don't open the $1,000 box then he will put the money in the second box and you'll end up $1,000,000 richer.
As Scott notes, people confronted with this problem fall into three categories: those that trust the Predictor and open only the second box, those that don't trust the Predictor and open both boxes, and those that consider the whole thing to be a paradox and therefore irrelevant.
He then goes on to propose a solution to the conundrum by defining "you" to be anything that can accurately predict your behaviour. This implies that the Predictor must be running a simulation of you that is, by the above definition, indistinguishable from the real you. The real you can then safely open only one box, knowing that the Predictor's simulation of you will make the same decision and you'll get the $1,000,000.
Scott concludes:
|
|
An important point about my solution is that it completely sidesteps the "mystery" of free will and determinism, |
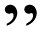
|
The only problem is that it trades the Predictor's paradoxical ahead-of-time omnipotence for a perfect simulation of a person. The latter is possibly more likely to exist, but is still rather improbable (I'm not sure how you go about measure degrees of impossibility).
I'd like to propose another solution that not only side-steps the mystery of free will, but also skips merrily past the need for either an omnipotent Predictor or a perfect clone/simulation of anyone. However, I should stress that this is entirely outside my area of expertise so it's quite likely that I'm just Plain Wrong™.
In this scenario we have the same two boxes but this time they contain cheques for $1,000 and $1,000,000 respectively. The lids to these boxes are wired up to contact switches. When you open the lid of one box the switch completes (or breaks) a circuit which causes a small explosive charge to detonate in the other box, destroying the contents (which is why we use cheques rather than real money). One final rule is that if you open both boxes then you must open the $1,000 box first. The end result is that you can have the contents of one box or the other but not both.
The mechanism implements an accurate simulation that faithfully reproduces the behaviour of the Predictor. Following Scott's logic, anything that can accurately predict the behaviour of another entity is indistinguishable from the real thing. So our mechanical and entirely deterministic Predictor is as good as the real thing but without the paradox. The game can be played exactly the same, but without the need to invoke the impossible.
One final point is to notice the similarity between this thought problem and that of Schroedinger's long-suffering cat. The money in the boxes in Newcomb's Paradox exists in a state of superposition, being simultaneously both a potential reward of $1,000 and $1,000,000. That is, until we open either box and collapse the waveform to just one possible value. Unlike Shroedinger's poor cat which stands a 50% chance of getting gassed through no fault of its own, no animals are harmed in the making of Newcomb's Paradox.